Copernican Derivations
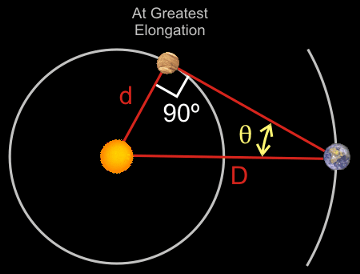
Calculating the size of an inferior planet's orbit is fairly easy – we need only one observation. Recall that if an inferior planet is at greatest elongation then the sun, the inferior planet, and the Earth (or other superior planet) are at a right angle. See Figure 1 at right. So measuring the angle of greatest elongation allows us to find the size of the inferior planet's orbit in terms of the size of the Earth's orbit. If θ is the greatest elongation, D is the radius of the Earth's orbit, and d is the radius of the inferior planet's orbit, then
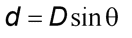
For convenience, astronomers use a unit of distance called an Astronomical Unit, or AU. One AU is the size of the Earth's orbit. Thus we can simplify the above formula to the following:
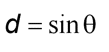
where d is measured in AUs.
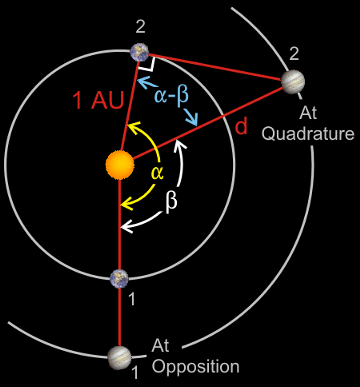
Determining the the size of a superior planet's orbit requires more work. One way to do this is to record the amount of time T it takes for a superior planet to go from opposition to the next quadrature. Then the Earth will sweep out an angle
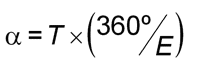
where E is the sidereal period of the Earth. See Figure 2 at right.
If P is the sidereal period of the superior planet, then it sweeps out an angle
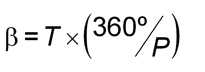
The difference of these two angles gives us the Earth-sun-planet angle at quadrature. Thus, if d is the radius of the superior planet's orbit, then
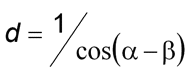
where d is measured in AUs.
You may have noticed that while we can determine the relative sizes of the planets' orbits using these methods, we don't have enough information to express these distances in more familiar units such as miles or kilometers. Finding the parallax of planets or asteroids is one way in which an observer can determine the size of an AU in more familiar units.
Recall that the synodic period is the period of the phases – that is, the time it takes a planet to return to the same position relative to the sun. The sidereal period is the time a planet takes to complete one orbit with respect to the stars or any fixed frame of reference.
If E is the sidereal period of the earth in days, then the earth moves at a rate of 360°/E degrees per day in its orbit. Likewise if P is the sidereal period of a planet, then the planet moves at a rate of 360°/P degrees per day. Let S be the synodic period of the superior planet.
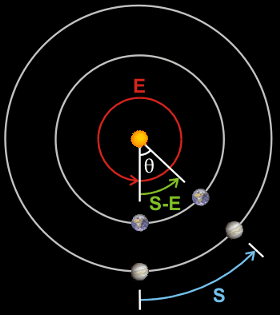
Copernicus correctly assumed that the more distant planets move more slowly in their orbits. So if we begin with the superior planet in opposition, the earth will have to complete one orbit and then go through an additional angle θ to catch up to the planet. Since the amount of time the earth takes to go though θ is S-E, we have θ=(S-E)×(360°/E). See Figure 3 at right. Since the superior planet also goes through θ in time S we can express θ as S×(360°/P). Equating these two expressions for θ we have
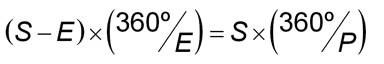
which we can simplify to get Copernicus's result:

For an inferior planet we can just interchange P and E since earth would have the outer orbit. This gives Copernicus's formula for inferior planets:
