Newton and Planetary Motion
In 1687 Isaac Newton published Philosophiae Naturalis Principia Mathematica, a work of immense and profound impact. Newton's pronounced three laws of motion and a law of universal gravitation. They were a united set of principles which applied not only to the heavens but also to the earth in a uniform way. Their simplicity and extremely broad applicability forever changed astronomy.
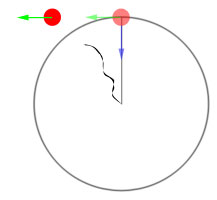
A body remains at rest, or moves in a straight line (at a constant velocity), unless acted upon by a net outside force.
The law of inertia did not originate with Newton, nevertheless it is integral to his system of mechanics. An object in motion will remain in motion unless something acts upon it. Because a planet is moving in an ellipse (i.e. not a straight line) this law states that there must be some “force” acting upon the planet. If there were no force, the planet would fly off in a straight line.
The acceleration of an object is proportional to the force acting upon it.
The first law says that if no force is acting on an object, it will remain in motion. The second law tells how the motion will change when a force acts upon the object. Velocity is how fast an object is moving (speed or magnitude) and the direction it is moving. Acceleration is a change in velocity. An accelerating object can either change how fast it is moving, the direction it is moving, or both.
For every action, there is an equal and opposite reaction.
The law can be more fully stated as, “Whenever one body exerts force upon a second body, the second body exerts an equal and opposite force upon the first body.” That is, when the sun pulls on a planet with the force of gravity, the planet pulls on the sun with a force of equal magnitude. But, because the sun is so much more massive than the planet, Newton's second law says that the sun will experience much less acceleration.
F = G m1 m2 / r2
Every object in the Universe attracts every other object with a force directed along the line of centers for the two objects that is proportional to the product of their masses and inversely proportional to the square of the separation between the two objects. While the law does not explain what gravity is, it does say how the force of gravity works. From this law and his laws of motion, Newton was able to derive all of Kepler's Laws of Planetary Motion.