Kepler's Laws of Planetary Motion
Johannes Kepler published three laws of planetary motion, the first two in 1609 and the third in 1619. The laws were made possible by planetary data of unprecedented accuracy collected by Tycho Brahe. The laws were both a radical departure from the astronomical prejudices of the time and profound tools for predicting planetary motion with great accuracy. Kepler, however, was not able to describe in a significant way why the laws worked.
The orbit of a planet is an ellipse where one focus of the ellipse is the sun.
An ellipse is defined by two focii and all points for which the sum of the distances are the same. The semimajor axis (a) is the long distance from the center to edge of the ellipse. If r1 and r2 are the distances from the focii to any point on the ellipse then r1 + r2 = 2a. The short axis is called the semiminor axis.
How “elliptical” an orbit is can be described by the eccentricity (e). The eccentricity is equal to the distance between a focus and the center (c) of the ellipses divided by the semimajor axis (a). That is, e = c/a. The NAAP Eccentricity Demonstrator shows ellipses for different values of a and c. Note c is always less than a by definition.
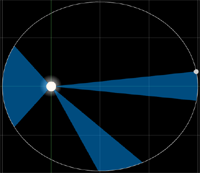
A line from the planet to the sun sweeps out equal areas in equal amounts of time.
With elliptical orbits a planet is sometimes closer to the sun than it is at other times. The point at which it is closest is called perihelion. The point at which a planet is farthest is called aphelion. Kepler's second law basically says that the planets speed is not constant – moving slowest at aphelion and fastest at perihelion. The law allows an astronomer to calculate the orbital speed of a planet at any point.
The period of a planet's orbit squared is proportional to its average distance from the sun cubed.
The average distance of a planet from the sun is equal to its semimajor axis (a). If the period (P) is measured in years and the semimajor axis (a) is given in astronomical units (the earth sun distance is 1 AU) then Kepler's 3rd can be written:
However, this equation is only good for our solar system. Isaac Newton was able to derive a more general form of the equation using his Law of Gravitation. Read more about Newton and Planetary Motion.