Finding Latitude and Longitude
One can easily determine latitude. Any star will consistently reach the same highest point in the sky. Its height in the sky changes with the observer's latitude. This concept was known and widely used from very ancient times. In the Northern Hemisphere the North Star was/is a popular choice. The angle the North Star makes with the horizon (α in the figure to the right) is the same as the observer's latitude.
Because one day is 24 hours long one can easily use time to calculate longitude. One hour of time difference corresponds to 15° of longitude (360°/24 hours = 15°/hour). Suppose an observer sets his accurate watch to 12:00 at noon in Greenwich, England and then travels a great distance. The observer then notices that the sun is highest in the sky at 4:00 according his watch. The observer then knows he is at longitude 60° W (4 hours ×15°/hour = 60°).
It should be pointed out that “noon” in general does not mean 12:00 PM. Rather, it is the time when the sun is highest in the sky. Because of the use of timezones the sun will be highest in the sky from about 11:30 AM to 12:30 PM local time for an observer. If longitude is known, the time of astronomical noon can be calculated.
For example, Lincoln, NE, is at longitude 96.7° W. 96.7°/(15°/hour)=6.4467 hours. Being Central Time, Lincoln is 6 hours away from Greenwich Mean Time, so astronomical noon is (6.4467 - 6) hours = 0.4467 hours = 26.8 minutes from 12:00. Thus “noon” in Lincoln, Nebraska is about 12:27 PM (1:27 PM during daylight savings).
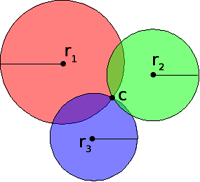
The finding of latitude and longitude by astronomical and temporal means has been somewhat replaced by the public availability of the Global Positioning System (GPS). The GPS works by means of trilateration. The system has several satellites (24) in geosynchronous orbit around the earth.
Distance to a satellite is determined by radio signals. The satellites constantly emit a string of code that essentially indicates time. When a GPS receiver receives the signal it merely needs to calculate how long it took the signal to arrive. The time difference multiplied by the speed of light gives the distance to the satellite.
If only the distance to one satellite is known, the observer can be anywhere on a circle (in three dimensional space it is a sphere, but we are constrained to be on the surface of the earth). If the distance to two satellites is known, the position reduces to two points. If the position to three satellites is known, the position relative to all three satellites is known precisely. This is the method of trilateration.
Because light travels extremely fast, the time difference between emission and reception of the GPS signals are of order nanoseconds. To maintain that level of accuracy requires atomic clocks. Each of the satellites has one. GPS receivers tend not to carry expensive atomic clocks. If a GPS receiver's internal time is a little off the three distances will still reduce to single point, but coordinates can still be wrong. However, if the distance to a fourth satellite is calculated, the distances won't intersect at a point unless the time is correct. Thus GPS receivers tend to need signals from four satellites – where the fourth signal serves to constantly readjust the receivers internal clock. If the time is correct (and the receiver is constantly readjusting its time) then the fourth satellite also allows altitude calculations.
Having the distances to four satellites gives a precise location relative to the four satellites. The receiver carries an internal data table of all the satellites locations. Being in geosynchronous orbits their positions are precise and stable. Even so, they are closely monitored and perturbations from their positions are also transmitted. Once the locations of the satellites with respect to the earth is known, the GPS receiver, knowing its position with respect to the satellites knows exactly where it is on earth.