Transitions
According to the theory quantum mechanics, an electron bound to an atom can not have any value of energy, rather it can only occupy certain states which correspond to certain energy levels. The formula defining the energy levels of a Hydrogen atom are given by the equation: E = -E0/n2, where E0 = 13.6 eV (1 eV = 1.602×10-19 Joules) and n = 1,2,3… and so on. The energy is expressed as a negative number because it takes that much energy to unbind (ionize) the electron from the nucleus. It is common convention to say an unbound electron has zero (binding) energy. Because an electron bound to an atom can only have certain energies the electron can only absorb photons of certain energies exactly matched to the energy difference, or “quantum leap”, between two energy states.
When an electron absorbs a photon it gains the energy of the photon. Because an electron bound to an atom can only have certain energies the electron can only absorb photons of certain energies. For example an electron in the ground state has an energy of -13.6 eV. The second energy level is -3.4 eV. Thus it would take E2 − E1 = -3.4 eV − -13.6 eV = 10.2 eV to excite the electron from the ground state to the first excited state.
If a photon has more energy than the binding energy of the electron then the photon will free the electron from the atom – ionizing it. The ground state is the most bound state and therefore takes the most energy to ionize.
Generally speaking, the excited state is not the most stable state of an atom. An electron has a certain probability to spontaneously drop from one excited state to a lower (i.e. more negative) energy level. When an electron drops from a higher level to a lower level it sheds the excess energy, a positive amount, by emitting a photon.
The energy of the emitted photon is given by the Rydberg Formula. This formula is essentially the subtraction of two energy levels. It is:
| Ephoton = E0( | 1 | − | 1 | ) |
| n12 | n22 |
where n1 < n2 and (as before) E0 = 13.6 eV. With the restriction n1 < n2 the energy of the photon is always positive. This means that the photon is emitted and that interpretation was the original application of Rydberg. It also works if the n1, n2 restriction is relaxed. In that case the negative energy means a photon (of positive energy) is absorbed.
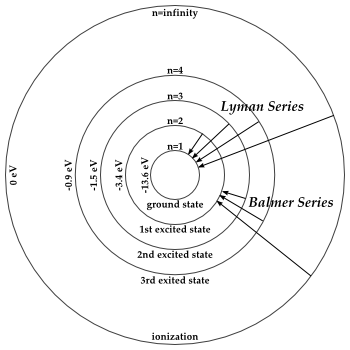
Long before the Hydrogen atom was understood in terms of energy levels and transitions, astronomers had being observing the photons that are emitted by Hydrogen (because stars are mostly Hydrogen). Atomic physicist Balmer noted, empirically, a numerical relationship in the energies of photons emitted. This relationship was generalized and given context by the Rydberg Formula. But the various discrete photon energies/wavelengths that were observed by Balmer were named the Balmer series.
It was later understood that the Balmer lines are created by energy transitions in the Hydrogen atom. Specifically, when a photon drops from an excited state to the second orbital, a Balmer line is observed. The Balmer series is important because the photons emitted by this transition are in the visible regime. The Balmer series is indicated by an H with a subscript α, β, γ, etc. with longest wavelength given by α.
As there are other transitions possible, there are other “series”. All transitions which drop to the first orbital (i.e. the ground state) emit photons in the Lyman series. All transitions which drop to the 3rd orbital are known as the Paschen series. The graphic to the right shows some of the Lyman and Balmer transitions graphically.
When Hydrogen is excited it emits light as photons de-excite. Or conversely, the Hydrogen will absorb photons of certain energies. The strength of the line from a source of Hydrogen will depend on how many electrons are in a particular excited state. If only very few electrons are the first excited state, the Balmer lines will be very weak. If many Hydrogen atoms are in the first excited state then the Balmer lines will be strong.
How many Hydrogen atoms are in what state is a statistical distribution that depends on the temperature of the Hydrogen source. The Thermal Distribution simulator demonstrates this.