The Doppler Effect
Wails and Redshifts
If you have ever heard the changing pitch of a siren as it passed by, you have experienced the Doppler Shift first hand. It is the change in frequency (and wavelength) due to relative motion of the source and observer. It applies to both sound and light (although they are somewhat different mathematically). Note that it can occur when either the source, observer, or both are moving – it is only necessary that the relative separation be increasing or decreasing.
In astronomy we are only interested in the application of the Doppler Effect to Light. In the image below two spaceships observe a star moving through space. The separation between the star and the spaceship on the left is increasing, so this ship will see light from the star redshifted – shifted toward longer wavelengths (lower frequencies). The separation between the star and the spaceship on the right is decreasing, so this ship will see the light shifted toward shorter wavelengths (larger frequencies).
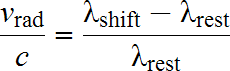
The Doppler Shift is governed by the equation to the right. The difference between the shifted (observed) value λshift and the rest (unshifted) value λrest can be used to calculate the radial velocity. This is the velocity along the line of sight between the source and observer – i.e. whether the object is moving toward us or away from us. The Doppler Shift only gives you information about this one component of velocity. Note that velocities away from us are considered positive and velocities toward us are negative.
The simulation below allows one to experiment with the speed and direction of a star’s motion relative to the earth and see the effect on an absorption line from the star’s spectrum. Experiment with this simulator. Note that there are many ways to get a given shift since the Doppler Effect only tells you about the radial component of velocity and there are many combinations of speed and angle which will yield a certain radial component. Astronomers typically observe the spectra of an object, make precise measurements of λshift for spectral lines for which they know accurate values of λrest, and then calculate the radial velocity using the Doppler Equation.