Detecting ExtraSolar Planets
Direct Detection
In addition to the 2.4 m Hubble Space Telescope, we now have many ground-based telescopes with apertures over 8 m. Why can't we use these incredibly powerful instruments to directly observe extrasolar planets? There are several obstacles which are simply too substantial even for these instruments. The separation between the extrasolar planet and its star is miniscule compared to the distances between stars. A star like the sun is about a billion times as bright as the reflected light from any extrasolar planet orbiting it. Telescope also blur the light from stars because of diffraction. Thus, extrasolar planets are simply too near their much brighter parent stars to be directly imaged from interstellar distances.
Indirect Detection
Astronomers have had much better success at indirectly detecting extrasolar planets. Instead of detecting the planet, they infer its existence by observing the effects that it has on its parent star. Remember that both the star and the planet move around a common center of mass. These efforts take three major forms:
Astrometric Methods look for the motion of the star (wobbles) about the center of mass. The animation shown below allows you to see the effects of the gravitational effects that the planets have on the sun looking down on the plane of the solar system. Experiment with a) Jupiter alone, b) Jupiter & Saturn, and c) Earth alone before trying other combinations.
These techniques have been used to identify binary stars with considerable success for many years and considerable effort has been exerted trying to detect exoplanetary systems astrometrically. However, no exoplanets have been discovered by this method to date. The wobbles are just too small to detect at the great distances of stars.
Radial Velocity Methods look for the periodic doppler shifts in the star's spectral lines as it moves about the center of mass. Thus, in the exoplanetary system seen to the right, an earth observer taking spectra would see:
- A blueshift (yielding negative radial velocities) when the star is moving toward Earth
- A redshift (yielding positive radial velocities) when the star is moving away from Earth
- No shift when the star is moving perpendicularly to the line of sight
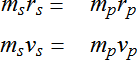
Many observations are combined to form the radial velocity curve for the star. Note that the period of the planet is equal to the period of the radial velocity curve. The amplitude of the curve is the speed of the star (vs) in a circular orbits.
Note that the size of the star's orbit has been exaggerated relative to the planet's orbit. The true size of the circular orbits is given by the center of mass equation. Since the planet is less massive than the star it moves more rapidly in a larger circle. Thus, if one were to increase the mass of the planet mp in the simulation above, the size of the sun's circle rs and the amplitude of the radial velocity curve would increase.
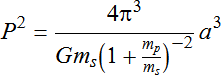
The period of the system is given by Newton's version of Kepler's 3rd Law. The average separation of the planet and star, a, is simply the sum of the radii for circular orbits. Typically the mass of the planet mp is small enough to ignore. However, then mp is large and ms is small it does have a noticable effect.
As of 2006, around 200 extrasolar planets had been identified using the radial velocity technique. In 2022, we are very near 1000.
Transit Methods look for the drop in the star's brightness as an exoplanet cuts across its disk along our line of sight. Even when the system geometry allows transits (eclipses) to occur they happen infrequently. Thus, in 2006 only a couple of exoplanets had been discovered through this method, although several discovered by the radial velocity method have been confirmed by observing transits. In 2022, several thousand exoplanets have been found using transit techniques largely by the Kepler and TESS space telescopes.