Center of Mass
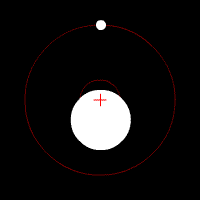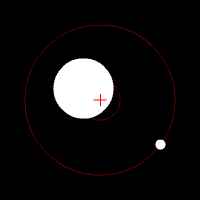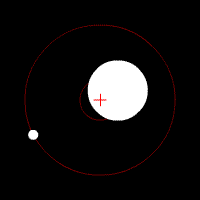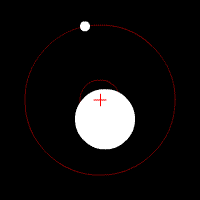
The center of mass is a very important concept when discussing extrasolar planets. It can be thought of as a “balancing point” between two objects of different mass. It is always found on the line between the two objects and is located closer to the more massive object. Both the star and the extrasolar planet will orbit around the center of mass (sometimes referred to as the barycenter).
The simulator below allows you to experiment with the masses of two objects and view the location of the center of mass. If the separation distance is set equal to the sum of the masses a relationship between the two masses and the two distances to the center of mass becomes apparent:
| m1 | = | r2 | . |
| m2 | r1 |
If the two masses are equal the center of mass must be halfway between the two masses. If they have different masses, the center of mass is always found closer to the more massive object. When one object is considerably more massive than the other, the center of mass may actually be inside the more massive object.
| xcm | = | m1x1 + m2x2 + m3x3 +… |
| m1 + m2 + m3 +… |
A general formula for calculating the location of the center of mass is shown to the right. The formula expresses the idea that adding up the product of each mass times its distance from the coordinate system origin and then dividing by the sum of masses gives the center of mass. You are free to place the origin of your coordinate system (the point where x = 0) wherever you wish, however it is usually most convenient to place it where one of the masses is located. We will be looking at the most simple version of the center of mass where there are two objects and we are interested only in one coordinate of the center of mass.
Example: Sun and Jupiter
The mass of the sun is about 333,000 Mearth. The mass of Jupiter is about 318 Mearth. Jupiter is 5.2 AU away from the sun. If we set the origin to be at the center of the sun, the center of mass in the following calculation is the distance of the center of mass from the center of the sun.
| xcm | = | (333,000 Mearth × 0) + (318 Mearth × 5.2 AU) |
| 333,000 Mearth + 318 Mearth | = | 0.005 AU |
It turns out that 0.005 AU is approximately the radius of the sun. Thus the center of mass of the sun/Jupiter system is about equal to the radius of the sun.