Definition of Scale Height
| Elevation | Density |
|---|---|
| 0 | ρ0 |
| H | (1/e)ρ0 = 0.368ρ0 |
| 2H | (1/e2)ρ0 = 0.135ρ0 |
| 3H | (1/e3)ρ0 = 0.050ρ0 |
| 4H | (1/e4)ρ0 = 0.018ρ0 |
Scale height is a general way to describe how a value fades away and it is commonly used to describe the atmosphere of a planet. It is the vertical distance over which the density and pressure fall by a factor of 1/e. These values fall by an additional factor of 1/e for each additional scale height H. Thus, it describes the degree to which the atmosphere “hugs” the planet.
Scale height is extremely useful for making “back of the envelope calculations”.
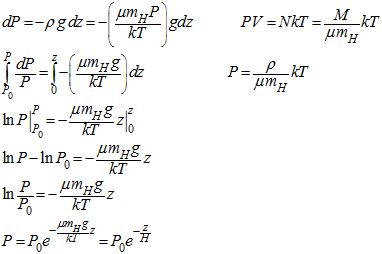
We can derive the scale height H by starting with the equation of hydrostatic equilibrium and using the ideal gas law to eliminate either pressure or density. Thus, although it is done here for pressure, scale height can be derived in terms of either pressure or density.
Note that the mass of a hydrogen atom (mH= 1.67 × 10-27) and Boltzmann's Constant (k = 1.38 × 10-23 J/K) are truly constants. The acceleration of gravity g and temperature T change slightly with elevation, but are treated as constant here. Note that μ is the average mass of an atmospheric particle (in units of a hydrogen atom mass). Thus, one normally does a weighted calculation for the masses of all constituents of the atmosphere.
We then integrate from the surface value of pressure to the elevation of interest, basically adding up the weight of the overlying atmosphere.
We now move pressure to one side of the equation, integrate, and solve an equation relating pressure and elevation.
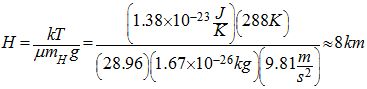
We can evaluate the average mass of Earth's atmospheric particles as approximately μ=(0.21)(32)+(0.78)(28)+(0.01)(40) = 29 by weighting its composition of oxygen, nitrogen, and argon. We choose a reasonable value for the average temperature (288 K) and an acceleration of gravity of 9.81 m/s2, and obtain a scale height of around 8400 m. It makes little sense to try and be more precise as slightly different values could be assumed for all of the inputs.
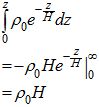
There is a second way to think about scale height, that is often more useful than the first. Let’s add up (integrate) all of the atmosphere from the planet surface out to infinity. This definition really only applies to density (and not pressure).
So we can think of the atmosphere as having constant density (at the ground level value) out to an elevation of H – a slab of constant density. This makes scale height extremely useful for making “back of the envelope calculations”.