Luminosity

The Luminosity of a Star

Luminosity is the total energy that a star produces in one second. It depends on both the radius of the star and on its surface temperature. One can calculate luminosity by finding the product of 1) how much energy each section of the surface of a star is producing (σT⁴, the Stefan-Boltzmann Law) and 2) the entire surface area of the star (4πR²). Thus, the luminosity of a star (σT⁴4πR²) would increase if one increased either the size R or the surface temperature T with temperature being the dominating factor. If we work in solar units indicated with a 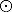symbol, we can ignore the constants and simply write L = R²T⁴.

For example, if a star has the same surface temperature as the sun and a radius that is twice as big, its luminosity must be L = (2 R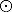)²(T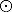)⁴ = 4L.

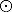One can experiment with the relationships between luminosity, temperature (spectral type), and radius with the Stellar Luminosity Calculator. Use the calculator to answer the following questions.

• What is the luminosity of a star that is the twice as big as the sun but has the same surface temperature?
• What is the luminosity of a star that is half as big as the sun and twice as hot?
• Estimate the size of a star that has the same surface temperature as the sun but produces 100 times as much energy.