Distance Modulus
Today parallaxes can only be measured for stars out to distances of 500 light-years. Since our galaxy is approximately 100,000 light-years in diameter, this only includes a small fraction of the total number of stars in the galaxy. How can the distances to stars even farther away be determined? One method that can be used is to compare their apparent brightness and luminosity.
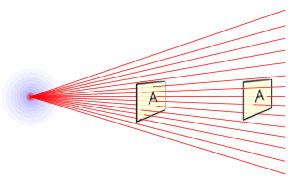
Suppose a friend in the distance is carrying a powered 100W light bulb. The further away the friend is, the dimmer the light bulb will appear. The closer the friend is, the brighter the light bulb will appear. So, by comparing how bright the bulb appears to how bright the light bulb is intrinsically, the distance can be determined. This is possible because of the inverse square law.
The diagram to the right visually depicts the inverse square law and light. The number of photons/rays going through each square is different depending on the distance of the square. Like parallax, this is a purely geometric effect.
Astronomers express the inverse square law effect with the distance modulus which is expressed in terms of magnitudes. The difference between the apparent magnitude (m) and the absolute magnitude (M) defines the distance to the object in parsecs. That is: m − M = −5 + 5 log10 d.
Try it: m − M = → d =
Additionally, the table below can be used for a quick check. Note that the 10, 16, 25, 40, 63 pattern repeats (with an increasing number of zeroes) and may be used to calculate values not contained in the table..
| m − M | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 15 | 20 | 25 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| distance (pc) | 10 | 16 | 25 | 40 | 63 | 100 | 160 | 250 | 400 | 630 | 103 | 104 | 105 | 106 |
One of the best known distance indicators are RR Lyrae Stars. These are pulsating variable stars – stars that change in brightness over time because they are periodically growing larger and smaller much like breathing. These stars pulsate because the release of energy from the outer layers of the star varies over time (due to a layer of partially ionized helium). When this ionized layer is close to the center of the star and hot – it becomes very opaque to the flow of radiation and the radiation pressure pushes it outward. When the ionized layer gets far from the star, it cools off and its opacity decreases. Radiation can now stream through and the layer falls back toward the center of the star.
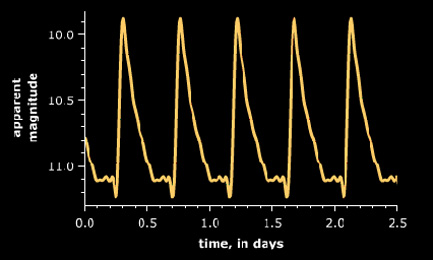
RR Lyrae stars are very good “standard candles”. These are objects where have a pretty good idea how intrinsically bright they are. It turns out that all RR Lyrae stars have absolute magnitudes very near MV = 0.5. However, since they are small, faint stars, they cannot be seen at large distances.
The figure to the right shows the variation in the apparent magnitude of the RR Lyrae star VX Her. Note that the average apparent magnitude is about 10.5. Thus, the distance modulus for this stars is (m - M) = 10.5 - 0.5 = 10, which corresponds to a distance of 1000 pc.
There are many other objects that astronomers use with the distance modulus to obtain distance. They all involve some method by which the astronomer uncovers the value of absolute magnitude M for an object and there are many different approaches used. The apparent magnitude m is then observed to obtain the distance.