Color Index

Even in prehistory astronomers noted that some stars were brighter than others. The differences in the brightness of stars was first systematically and numerically defined by the second century B.C. by Hipparchus. He rated the stars on a scale of 1 to 6 with 1 being the brightest stars and 6 being the dimmest stars. But the scale was not linear, it is logrithmic.

A logarithmic scale is useful for the eye because the human eye's response, how “bright” things are, is not linear. Suppose there is star A that has a certain brightness. Star B puts out 10 times the photons of star A. Star B will not be observed as being 10 times brighter than star A. And if Star C puts out 100 times the photons of star A, star C will not be 100 times brighter than star A. Rather, star C will be brighter than star B by as much as star B is brighter than star A. Hipparchus's system reflected this behavior.

Today the logarithmic difference in “brightness” is mathematically defined, but not necessarily in a way that modern astronomers would have done so. In 1856 astronomer Pogson reasoned that a class 6 star was about 100 times brighter than a class 1 star. So a class 2 star would be 2.512 times brighter than a class 1, a class 3 star 2.512×2.512 brighter than a class 1, and a class 6 2.512⁵ = 100 times brighter than a class 1 star. 2.512 ≈ 100^1/5.

And because of Hipparchus and Pogson, the observed “brightness” is defined with such a logarithm. Specifically:

where F is flux, or the number of photons being measured and F₀ is a normalizing factor. It is important to note that lower numbers are brighter than higher numbers. m = -2 is 100 times brighter than a m = 3 star.

How bright a star is through a particular filter is the color magnitude. A commonly used system is the UBVR system as mentioned in the filters background page. When a number is given for U, it is the apparent magnitude of the star as seen through the U filter. In other words, U is how “bright” the star is for a limited region of the spectrum. If two stars were the same size, the same distance away, and the same temperature, they would both have the same value of U. And the temperature is the primary indicator of the “color” of the star as temperature changes the blackbody curve of the star. The graph below shows color vs. temperature.

Color and temperature relation for idealized blackbodies.

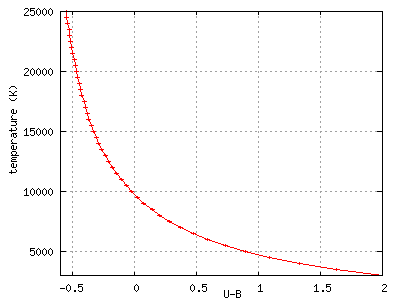
How bright we see a star being depends on, among other things, how far away the star is. So two stars of the same temperature will have different color magnitudes. This makes the number not as useful as it could be. But because of the way logarithms work, if one takes the difference of two magnitudes, complications such as distance and the size of stars is removed leaving temperature as again the primary influence of the star's color. Consequently, astronomers use “color indices” to talk about the color (and hence temperature) of stars.

So the colors of stars are described by quantities such as U-V and B-V. But in another fairly arbitrary choice of astronomers, each color magnitude is normalized differently (that is, they each have a different F₀). A common choice is normalizing so that the star Vega (which is about 10,000 K) has color indices U-V = B-V = 0. It is possible for each observatory to use slightly different normalizing factors as corrections for local atmosphere and instruments are used. But, in theory, all observatories will give the same color index for each star, even if their color magnitudes may be a little different.