Escape Velocity
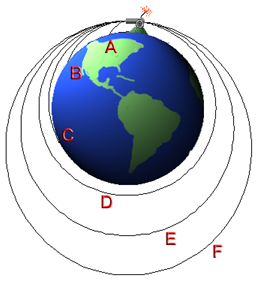
There is the old adage that “what goes up, must come down”. When thinking about gravity, Isaac Newton developed the concept of an orbit. He imagined a cannon on top of a tall mountain. When the cannon ball is shot, the cannon ball travels a certain distance (path A). If more gunpowder is used, the cannon ball is shot with greater speed and travels even farther (paths B and C).
Knowing that the earth was round, Newton thought about the path the ball would take if it were shot with even greater speed. In his simplistic thought experiment, the ball could actually curve around the earth and hit the back of the cannon (path D). Such a fast moving ball would be said to be in a circular orbit. Such an object will never come down – they continually “miss” the earth since the Earth’s gravity is continually redirecting the ball. Nevertheless, they are still bound to the earth and cannot escape. Firing the cannon ball with even greater speeds results in elliptical orbits (paths E and F).
Now instead of shooting the cannon sideways, imagine a similar experiment where the cannon is shot straight upwards. Each time more gunpowder is added, the cannonball travels to a greater height and takes longer to come back down. In the limit of our thought experiment the ball can go so high that it would take forever to come back down. Such a ball is said to have “escaped” as it will never return.
The speed necessary to launch an object up such that it will never come back is well defined for masses because the basics of how gravity works is well understood. This speed is called the “escape velocity” and it is defined as:
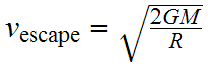
Note that the escape velocity depends upon both the mass M and radius R of a body and uses Newton's Gravitational Constant G = 6.67 × 10-11 N·m2/kg2. Its value for the Earth is 11,200 m/s. A particle will escape if it has a “one-time” vertical component of velocity greater than this value. Note that this is very different from the method by which rockets escape from the Earth by continually providing thrust. Rockets escape even though their speeds are much less than the escape speed.