Elongations and Configurations

In Copernicus's heliocentric model the planets orbit in circles around the sun. One may wonder how Copernicus determined the order of the planets and the size of their orbits – after all, he had no benefit of pictures from spacecraft or even a telescope. He determined these things by measuring elongation. Elongation is the angle between the sun and a planet as seen by an observer on earth. Imagine that you could see Venus and the sun at the same time. To measure the elongation of Venus, you could hold a piece of paper so that its flat edge is in line with the two objects. Then you would draw a line pointing to Venus and a line pointing to the sun. Measuring the angle between the two lines gives you the elongation of Venus. (Looking at directly at the sun is not recommended!)
For instance, if the sun and a planet are at the same point then the elongation is 0°. If a planet is at the opposite point in the sky from the sun, it has an elongation of 180°. However, some planets will never have such an elongation. To see why, we need to consider the difference between inferior planets and superior planets.
If we could look down on the Solar System from a distant point in space we would see that some planets are closer to the sun than the earth, and some are farther away. The ones that are closer are called inferior planets. The ones that are farther away are called superior planets. Also note that from this perspective, elongation is the angle between the sun, the earth, and a planet. See Figure 2.
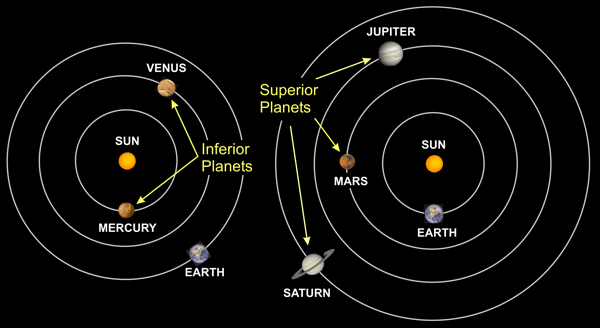
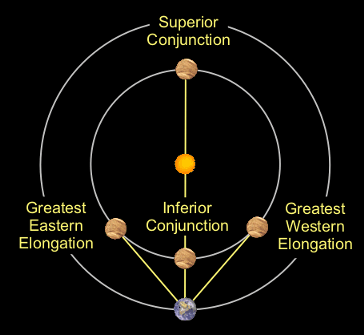
Looking at Figure 3 you should be able to see why an inferior planet can never have an elongation of 180°. If it did, that would mean the planet is farther away from the sun than the earth. Instead, for inferior planets there is a limit called the greatest elongation. This is the maximum angle that ever occurs between the sun and an inferior planet, and it depends on the planet's distance from the sun. Observing that a planet never has an elongation of 180° means that it must be an inferior planet, and this is how Copernicus knew that Venus and Mercury are closer to the sun than the earth. Further, by using geometry Copernicus was able to determine the distances of these planets from the sun based on their greatest elongations. (See the advanced page for more detail.)
Note that there are two points at which an inferior planet is at greatest elongation. We differentiate these by observing whether the planet is west or east of the sun at that time. Also note that there are two different configurations in which an inferior planet has an elongation of 0°, and these are given different names. When the planet is between the sun and the earth, we say it is at inferior conjunction. When the planet is on the other of the sun as seen from earth, it is at superior conjunction. (This terminology can be confusing since the words inferior and superior are both used to describe type of planets as well as elongation configurations – which is why an inferior planet can be at superior conjunction.)
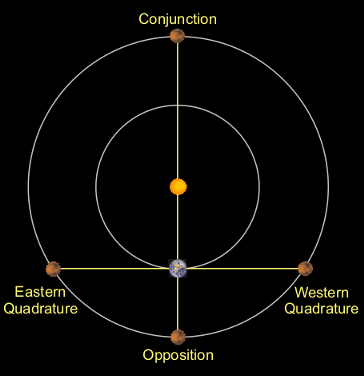
Unlike inferior planets, superior planets can have any elongation value between 0° and 180°. When a superior planet has an elongation of 0°, we say it is at conjunction (since there is only one type of conjunction for superior planets, we do not need to use the term superior conjunction). An elongation of 180° is called opposition, since the sun and the planet are on opposite sides of the earth. Another special configuration for superior planets is quadrature, which occurs when the planet has an elongation of 90°. As with greatest elongation, we can specify that a planet is at eastern quadrature or at western quadrature.
Thus, if a planet ever reaches opposition we know it must be a superior planet. This is how Copernicus decided Mars, Jupiter, and Saturn are farther from the sun than the earth. (The planets Uranus, Neptune, and Pluto were discovered in 1781, 1846, and 1930, respectively, so Copernicus never knew about them.) The size of an superior planet's orbit can also be determined from elongation measurements. (See the advanced page for more detail.)
Sidereal and Synodic Periods
By observing the elongations of the planets Copernicus was able to figure out how far each planet is from the sun. However, he still needed to know how long each planet takes to orbit the sun. The time it takes to complete an orbit is called the sidereal period. If we are at fixed point in space and had enough time, all we would need to do is to start a stop watch and record how long it takes for a planet to return to the same position as when we started.
For a human on the earth, this is not practical. First, planets can take a long time to complete their orbits (for instance, Saturn's sidereal period is over 29 years). But a more important factor is that the earth is orbiting the sun along with the other planets. We do not have a fixed frame of reference, so it is impossible to measure the sidereal period directly.
Fortunately, elongation provides an indirect way to calculate the sidereal period. What we need to do is measure the synodic period. The synodic period is the time it takes for a planet to make a complete cycle of elongation configurations. For instance, we can measure the synodic period of Mars by recording the time it takes for Mars to go from one opposition to the next opposition. For Venus, we can record the time it takes to start at and then return to its greatest western elongation. It does not matter which elongation configuration we choose – all that matters is the time it takes to return to the same elongation configuration.
Copernicus was able to show that the synodic period of a planet (S), the sidereal period of the planet (P), and the sidereal period of the earth (E) are related by one of the following formulas:
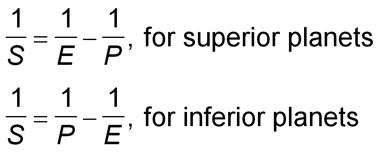
The sidereal period of the Earth has long been known to be about 365.25 days. So the above formulas let us calculate the sidereal period of any planet by measuring its synodic period. (These formulas are derived on the advanced page.)