Parallax
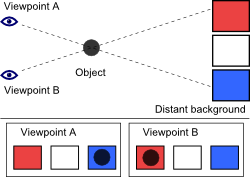
Parallax is the apparent shift of an object's position relative to more distant background objects caused by a change in the observer's position. In other words, parallax is a perspective effect of geometry. It is the observed location of one object with respect to another – nothing more.

Humans are already very accustomed to parallax as our two eyes provide a small parallax effect known as stereo vision. The left eye has a slightly different point of view than the right eye. This can easily be seen by looking at the location of a nearby object relative to more distant objects first throught one eye alone and then through the other eye. The brain uses the two images to create depth perception (along with several other clues). The parallax contribution to depth perception only works for close objects. When an object is far away, the shift in position of a foreground object to the even more distant background becomes too small for the eyes and brain to register.
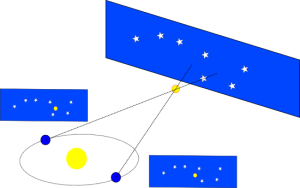
Stars are very far away – yet some stars are closer than others. Do these closer stars exhibit parallax? The answer turns out to be yes, but the parallax is very small – far smaller than can be seen with the naked eye. The first successful measurements of a stellar parallax were made by Friedrich Bessel in 1838, for the star 61 Cygni.
To create the largest parallax effect, we need to have the largest shift in position for the observer. The largest shift possible from the Earth is 2 AU – the diameter of the Earth's orbit. This shift corresponds to two positions of the Earth 6 months apart. Assuming the star being observed doesn’t move much in 6 months (a very good assumption), an astronomer need only look at its position once, wait 6 months and measure the position again relative to the much more distance stars.
Because the parallactic baseline would be given in astronomical units, astronomers also defined a distance in terms of that baseline known as the parsec. It is defined as the the distance at which a baseline of 1 AU subtends a parallactic angle of 1 arcsecond (1/3600th of a degree).
The diagram below allows one to explore how parsec is calculated. It is nothing more than basic trigonometry. Note that the diagram is not to scale. The real triangle is much, much longer (it is over 200,000 times longer than it is tall).
Parallactic angles of stars are difficult to measure. The European Space Agency launched the Hipparcos satellite which was in operation from 1989 to 1993. It could measure a parallactic angle of about 0.001 arcsecond. Before Hipparcos, literally only a hundred or so parallactic angles were known to any accuracy. Due to Hipparcos, the distances to several thousand stars are known to better than 5% accuracy.
Several thousand stars, however, is still only a very small fraction of the galaxy. The next satellite planed is Gaia (Global Astrometric Interferometer for Astrophysics). It aims to increase the angular resolution of Hipparcos by a factor of over a 1000. Scheduled to be launched in 2011, Gaia will dramatically increase the number and accuracy of known distances to stars in the Milky Way.